|
|||||||||||
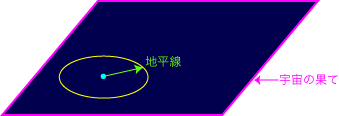
遠くを見ることは昔を見ることになります。地球を中心としてどこまで見えるか?と言う問いは、どれだけ昔が見えるか?と同じことで、電子が原子核にとらえられ、宇宙が晴れ上がって光子が自由になった時代が「見える限界」です。 光以外のものを通してでも、ともかく私たちと何らかの関係があり得る距離としては、前に紹介した「地平線」までと言うことになります。宇宙の長い歴史の中で、宇宙が晴れ上がるまでの時間は宇宙の年齢に比べるとずっと短いですから、地平線までが見える限界と思っても差し支えないでしょう。 でも皆さんの知りたいことは、「地平線の向こう側がどうなっているか?」なのでしょうね。私たちが地球の上で見る、いわゆる地平線の向こう側のことはよく知っているわけですが、地平線の定義から分かるように、向こう側を知ることはできません。大航海時代の人々と同じような気持ちかも知れませんね。しかし宇宙の地平線の向こう側は「原理的に」見ることができないのです。 そこで、これまでの理論や観測事実を頼りに想像するしかありません。 空間は3次元ですが、想像したり図に描いたりするのが難しいので、2次元の空間を考えましょう。
つまり、私たちのいる場所は特別な場所ではなくて、私たちが観測することは他のどの場所でも観測できる、と言うのが一様性でした。また、どの方向を見ても同じに見えるという等方性が成り立つとすると、例えば西の方だけ宇宙の果ての影響が見えていて東の方は見えない、と言うことをあり得ません。この2つの大前提が成り立つとすると、宇宙は無限に広いか、有限の広さの場合には球の表面のようになっていなくてはなりません。  一様・等方性を満たす無限に広い面は、平面と双曲面があります。何れにしても宇宙が始まったときに無限大の空間から始まったというのは奇異な感じがするかも知れませんが、「始まりの瞬間」が分かっていないので、このような可能性も否定できません。 これでは気持ち悪い(?)ので、「一様・等方性を捨ててしまえ!」と考えるかも知れませんが、そうするとビッグバン理論で説明できた様々な観測事実を改めて検討する必要が生じます。さらに、私たちが「特別な場所」にいることも説明しなくてはならないでしょう。どちらがより自然か?というのは人それぞれでしょう。ここでは、一様・等方性が成り立つとして話を進めましょう。 |
|||||||||||
3つの図形をイメージするとそれぞれ、下の3つの図になります。  宇宙のエネルギー密度と宇宙の形には次のような関係があります。
現在の宇宙の密度はほとんど臨界密度に等しいので、この3つのうちのどれであるかは断定できませんが、閉じた宇宙(球面)にせよ開いた宇宙(双曲面)にせよ曲率がほとんど0に近い場合になっているでしょう。例えば、球面(閉じた宇宙)で曲率が大きい、つまり半径が小さいと、望遠鏡で遠くを見ると自分の頭の後ろが見える、とか、宇宙船で直進すると元の場所に戻っているということがあるのですが、半径が十分大きくて、現在の地平線よりもずっと大きければこのようなことは起こりません。 結局、宇宙のエネルギー密度が正確に分からないので、ほとんど平坦であるが、どの形になっているかは断定できません。 |
|||||||||||