|
||||||||||||||||||||||||||||||||||||||||||||
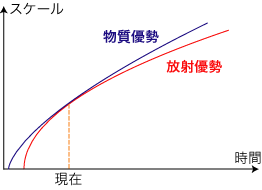
| 宇宙の始まりがよく分からないので、正確には年齢を決めることは出来ないのですが、宇宙が始まって約1秒ほどで元素合成が起こるように、宇宙の始まりの謎はごく初期の非常に短い時間に凝縮されています。 宇宙初期の放射優勢の時代ですら1万年程度ですので、100億年を超すと言われる宇宙の歴史から見ると100万分の1以下です。従って、「年齢」を考えるときには、物質優勢の時代がほとんどを占めていて宇宙のごく初期は無視しても良いでしょう。 では、宇宙の年齢を決めるにはどうすれば良いかというと、宇宙の歴史を逆にたどって、大きさがほとんど0になるまでの時間を計算すれば良いのです。つまり、現在のハッブル定数の値から始めて、それぞれの時刻でのハッブル定数を求めて、宇宙のスケールがほとんど0になるまで時間をさかのぼります。
ところが、宇宙の膨張の仕方は、宇宙の中のエネルギー密度によって決まっています。また、エネルギー密度と宇宙のスケールの間にはある関係があります。前に見たように、放射のエネルギー密度はスケールの4乗に反比例し、物質のエネルギー密度はスケールの3乗に反比例します。従って、宇宙のエネルギーの中身が何であるかによって、時間をさかのぼるときの宇宙のスケールの変化の仕方が違います。
|
||||||||||||||||||||||||||||||||||||||||||||
|
エネルギー密度が大きいと、重力の引力がはたらいて、現在は膨張している宇宙でも将来収縮するようになります。エネルギー密度が小さいと、そのまま膨張を続けます。将来宇宙が収縮するか膨張を続けるかの境目になる密度のことを臨界密度といいます。この臨界密度は、後に述べる宇宙の形を決める重要な要素でもあります。 現在の臨界密度は質量に換算すると約10-29g/cm3です。 それでは、実際の宇宙のエネルギー密度はいくらなのでしょう?それが分かれば、宇宙の将来も分かるかも? ところが地球上で固体や液体の密度を測るほど簡単に、宇宙のエネルギー密度を測ることは出来ません。それは、ハッブル定数の測定と、フリードマン方程式を用いて、宇宙の膨張の仕方から決めています。その結果、誤差が大きいのですが、誤差の範囲内で臨界密度と一致します。但し、「誤差の範囲」がありますから、宇宙の運命は微妙なところで、これだけの情報では未だ分かりません。 でも、臨界密度に非常に近いのには何か理由があるのでは?と考えたくなるのが物理屋の性分です。実は、そのような理論も考えられています。 |
||||||||||||||||||||||||||||||||||||||||||||
これまで、エネルギーの種類として、物質(質量を持つもの)と放射(質量のないもの)に大別してきましたが、ここ数年の精密な観測により、現在の宇宙の膨張の仕方を説明するには、もう1つ別の形態のエネルギーが必要であることが分かってきました。非常に遠方の星の見え方や、宇宙背景放射の非常に小さな温度揺らぎの観測の精度が飛躍的に向上し、それぞれのエネルギーが占める割合が詳しく分かるようになってきたのです。特に、ここ2、3年(2003年現在)の進展はめざましいものがあります。その時代に生きているのですから、幸運ですね。 では、どんなエネルギーかというと真空エネルギーと言われるものです。ダークエネルギーとも言われます。これは宇宙のスケールによらずに、空間をみたしています。私たちの日常に関係している物理法則には、この真空エネルギーは無関係です。例えば化学反応や原子核反応でエネルギーを取り出すことをしますが、それは反応前後のエネルギーの差であって、エネルギーの絶対値は関係しません。ところがアインシュタイン方程式(従って、フリードマン方程式)はエネルギーの絶対値に依存しています。
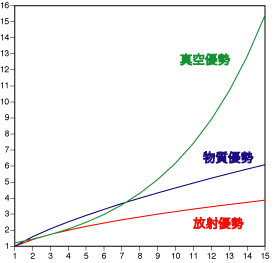
では真空エネルギーがあると、宇宙の膨張の仕方はどうなるのでしょうか。その特徴をとらえるために、まず宇宙のエネルギーの全てが真空エネルギーであるとしましょう。このとき、空間のスケールは時間の指数関数のように急激に増加します。「指数関数」を説明するために物質優勢や放射優勢の場合のスケールの増え方と比較してみましょう。
真空エネルギーの割合がこのように大きいのはちょっと驚きです。時間をさかのぼると物質や放射のエネルギー密度の方が急速に増加するので、これまでにお話ししたビッグバン理論、特に放射優勢の時代に起こったことの内容は変わらないのですが、宇宙の年齢や宇宙の将来についての予想を大きく変更しました。 物質のエネルギー密度が100%の場合と、真空エネルギーが73%ある場合にスケールの時間依存性を計算し、現在の時刻でグラフの傾き(ハッブル定数)が一致するように重ねると下のグラフのようになります。 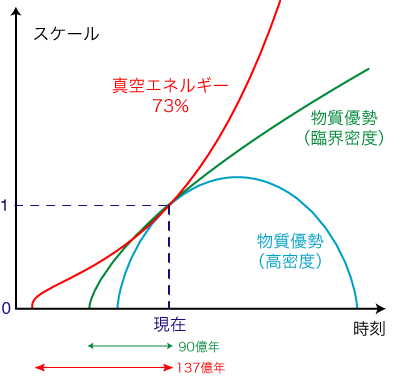 真空エネルギーが多いほど、曲線の初期の立ち上がりが緩くなるので、宇宙の年齢は長くなります。臨界密度のほとんどが物質密度であると考えられていたときは、宇宙の年齢は90から100億歳と思われていたのですが、最新の観測データに基づくと、
になります。 このように、宇宙の年齢に関してはかなりよく分かってきました。 |
||||||||||||||||||||||||||||||||||||||||||||
銀河の星やその速度の分布からも、目に見えない質量を持った物質が必要であることは以前から言われていました。目に見える物質の6倍近くあるわけですから、星や銀河の形成に重要な役割を果たしたと考えるのは自然でしょう。 では、ダークマターの正体は何なのでしょうか? 活動を終えた星やブラックホールと思われるかも知れません。「バリオン的物質が4%」というのは、上に述べたように宇宙背景放射の観測から得られた値ですが、元素合成に必要なバリオン数とも一致していますので、見えない星まで含めた「全てのバリオン的物質」の密度です。従って、見えない天体は陽子・中性子からできているとするとバリオン的物質に含まれます。ダークマターは次の性質を満たす、バリオン的でない粒子から出来ているはずです。
一方、質量が大きく、速度が光速に比べてずっと小さい粒子からなるダークマターは、冷たいダークマターと言われます。既知の素粒子の中には、上の3つの性質を満たし、質量が大きいものはありません。例えば中性のヒッグス粒子は1.と2.の性質を持つのですが、クォークやレプトン、ゲージ・ボソンに崩壊してしまいます。そこで、冷たいダークマターの候補としては未知の粒子が考えられますが、むやみに都合の良い粒子を加えるわけにはいきません。素粒子の標準模型を拡張した理論で、安定な中性粒子を含むものとしては、ある種の超対称性理論があります。この理論は現在、精力的に研究されています。 このようにダークマターは必要であることは分かってきましたが、その正体はまだ分かっていません。 |
||||||||||||||||||||||||||||||||||||||||||||