私たちが星空を見ている限りは宇宙はじっとしていて、無限の広がりを持っているような気がします。ところが「夜は暗い」という当たり前の事実がこのことを否定しているのです！

このことを理解するために次の簡単な光の性質を思い出しましょう。

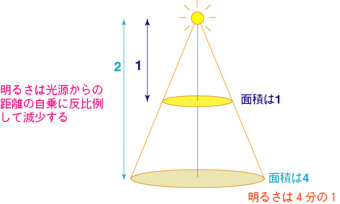
次に、星や銀河の分布が一様で無限に広がっていて、時間的に変化しないとします。

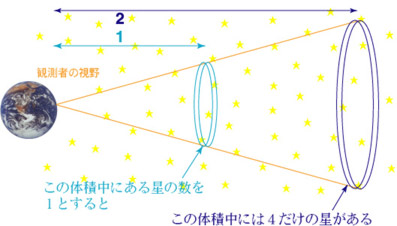
このとき地球上の観測者が見る一定の視野の中にやってくる光を考えます。濃い青の薄い円板の中にある星は水色の薄い円板の中にある星に比べて、その観測者より２倍遠いので星の明るさは４分の１です。ところが円板の円の面積は４倍ですので（中学校で習った三角形の相似の話を思い出してください）、星の分布に濃い薄いが無ければ（一様ならば）、そこには水色の円板よりも４倍の数の星があります。
そうすると濃い青の円板にある星全体から観測者の目に入ってくる光と、水色の円板にある星全体から観測者の目に入ってくる光の量は同じなのです。
ところが無限の彼方まで続くこのような円板のすべてから同じ量の光が観測者の目に入ってくる訳ですから、空はいつも白く明るい、ということになってしまいます。
これは明らかに現実と矛盾しています。

従って「星や銀河の分布が一様で無限に広がっていて、時間的に変化しない」とした仮定のどれか（あるいは幾つか）が間違っています。
しかし前節で述べたように宇宙が一様であることを認めるとすると、宇宙は定常で無限に広がっているわけではないことになります。

実際1929年に、この事実を支持する発見がありました。
それはハッブル（E. Hubble）によって発見された

というハッブルの法則です。等方性のためにすべての方向に、です。

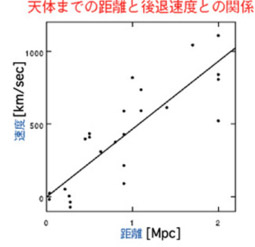
ハッブルは遠くの天体までの距離を横軸に、その天体の後退速度を縦軸にとり、それまで知られていた天体のデータをグラフにしてみました。 距離の単位はMpc（メガ・パーセク）で 1Mpc = 326万光年 です。 それにしてもハッブルはこれだけの荒いデータで思い切って直線を引いて、よく「比例関係」を見いだしたものです。
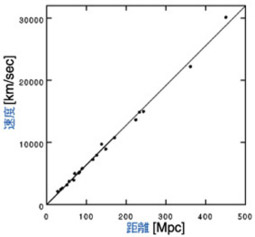
遠くの天体までの距離やその天体の速度をどうやって測るかはここでは詳しく述べませんが、最近はそれらの精度が上がり、さらに遠くの天体についても観測できるようになりました。 右の図は1996年までのデータを使って、上のハッブルが最初に描いたグラフを書き直したものです。 グラフのスケール（目盛）に注意してください。200倍以上遠くの天体について観測できています。 これを見れば「比例関係」があるのは疑いようはないでしょう。

です。つまり、1Mpcだけ遠い星ほど秒速約71kmだけ後退速度が大きいということになります。

この法則の発見により「夜が明るくない」ことが説明できます。ある程度遠い星は地球から見て光速（秒速30万km）より速く遠ざかるのでその光は地球に届かないでしょう。これで一安心？!

いえいえ、ちょっと待って下さい。地球から見て星が遠ざかっている、しかもその速度は遠いものほど大きい。

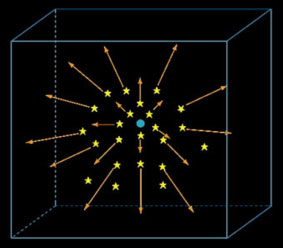
このハッブルの法則は未来永劫変わらないと思われていた宇宙の描像を根底から覆すものでした。 このことをイメージすると、左の絵のように、宇宙空間の中で星が地球を中心に爆発するように広がっていくような様子を思い浮かべるかも知れません。地球で観測するハッブルの法則だけを説明するならこの絵でも良いかも知れませんが、これでは地球を特別扱いしています。 前の節でお話しした宇宙の一様性のことを思い出して下さい。宇宙のどの場所も対等なのですから、地球以外のどこででもハッブルの法則が成り立っていなければなりません。 果たしてこのようなことが可能なのでしょうか？

これを絵に描いて説明するために、私たちの世界は３次元ではなくて２次元であるとします。私たちは「面」の世界に住んでいてその外側を認識できないとします。

例えば球形のゴム風船の上にいる蟻を想像して下さい。 蟻の世界はこの風船の表面だけで、風船の外部や内側のことを感じることは出来ないとします。 そして星や銀河などの天体、もちろん私たちの地球もこの風船の表面に張り付いていると想像して下さい。 そして風船が球形を保ったまま膨らんだとしましょう。

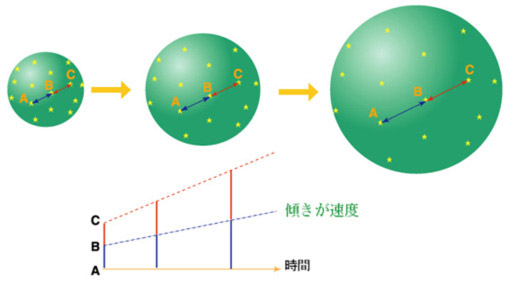
この絵から分かるように球の表面の２つの点は風船が膨らむに従って互いに遠ざかりますが、その速度は２つの点が離れていれば離れているほど大きくなります。Aから見てBよりも２倍遠いCの方が後退速度は２倍になっています。
つまりハッブルの法則が成り立っているのです！
またこの事情はA地点だけでなく、この球の表面（＝今考えている私たちの宇宙）至る所で成り立っています。球の表面はどこでも対等だからです。

この状況は球の大きさによりませんし、球でなくても平面（＝半径が無限大の球）でも同じです。

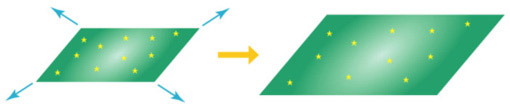
こうして蟻が住んでいる面（球面や平面）そのものが膨張すればハッブルの法則は説明できます。
ハッブルの法則が宇宙の至るところで成り立つならば単なる星の運動としては説明できないのです。

この考え方を現実の３次元の私たちの宇宙に適用すると、宇宙空間そのものが膨張する事になります。
上の絵では３次元空間の中で球面（または平面）が一様に広がっています。しかし蟻にしてみれば３次元目の広がりを感じることが出来ないので、３次元は必要ありません。絵に描いて表現できませんが、３次元空間そのものが膨張する場合も４次元空間を考えても良いのですが、それを感じる方法を知らなければ必要は無いのです。

「空間が膨張する」というのは日常の感覚では理解しにくいのですが、このことはハッブルの法則以前から予言されていました。

天体の運動は重力（万有引力）によって説明できることは古くにニュートンによって明らかにされていました。
この重力の法則の現代版がアインシュタインの相対性理論で、重力の大きさを空間の曲がり方と関係付けています。
ニュートンの重力の法則は、重力の大きさが物体の質量で決まると言うように、相対性理論では空間の曲がり方はその中にあるエネルギー（質量もエネルギーの一形態です）で決まることになっています。

1922年にフリードマン（Friedmann）がアインシュタインの理論（アインシュタイン方程式）をエネルギーが一様・等方に分布する場合に適用したところ、空間の大きさが時間とともに増大することを示しました。そしてその増大の仕方がハッブルの法則と一致していたのです！

ハッブルはフリードマンの結果を知っていて、上のグラフで無理矢理「比例関係」を示すような直線を引いたとも考えられますね。

宇宙空間の膨張の仕方はその中のエネルギーで決まっている、といいました。時間をさかのぼると宇宙の大きさは小さくなって行き、どこかで大きさが０になることがあるかも知れません。また未来には宇宙はどうなるのでしょう？

これらの問題に答えるには、その時々でのエネルギーの量（密度）と形態（質量、光など）を知る必要があります。

次に宇宙を満たしているエネルギーについて考えてみましょう。